计算几何初步

March 19, 2011

以前看到计算几何的题目就心虚，USACO的计算几何题目基本都跳过了，今天认真看了一下，发现其实计算几何没有想象中的那么难。本来做到USACO的fence3的题目，其中关键的一步就是求点到线段的最短距离，我本来想用解析几何做，也就是求出点到直线的距离，不过这样做我推导了半天，十分繁琐，后来想用海伦-秦九昭公式先算出三角形的面积，然后就出来了。但是看了TC的Algorithm Tutorial，发现原来求解的过程这么的简单。。。

首先介绍计算几何中的基本概念：

1.向量，这个不用多说了，最基本的概念。

2.点积(Dot Product),也叫数量积，是接受在实数R上的两个向量并返回一个实数值标量的二元运算。这里只考虑2维的向量，A=[x1,y1],B=[x2,y2],则A*B=x1*x1+y1*y1;在欧式几何空间中，点积可形象的表示为A*B=|A||B|cos(θ),θ为两个向量之间的角度，图示如下。

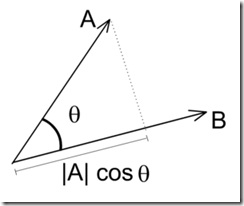
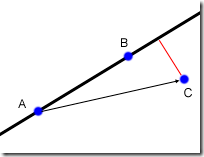
image

根据这个公式，可以计算向量的夹角，所以，一般点积可以判断点之间的关系。如下图，如果AB*AC<0,则说明90<θ<270,则说明C点在A的外面。

image

根据点积的概念可以写出计算点积的代码：

double dot(point a,point b,point c)//ab*ac
{
    point ab(b.x-a.x,b.y-a.y);
    point ac(c.x-a.x,c.y-a.y);
    return ab.x*ac.x+ab.y*ac.y;
}

3.叉积(Cross Product),也叫向量积，需要注意的是ABxAC的结果也是一个向量，而且方向和这两个向量都垂直，由于只考虑平面，所以这个方向并不做考虑，有兴趣再看。

设AB=[x1,y1],AC=[x2,y2],则ABxAC=x1*y2-x2*y1;

ABxAC=|AB||AC|sin(θ),这个结果在平面上可形象的表示为：

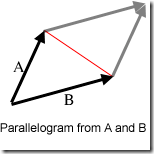
image

这个平行四边形的面积，当然是不考虑其方向。

同理，叉积的代码如下：

double cross(point a,point b,point c)//abXac
{
    point ab(b.x-a.x,b.y-a.y);
    point ac(c.x-a.x,c.y-a.y);
    return ab.x*ac.y-ab.y*ac.x;
}

4.点到线段的距离，点到直线的最短距离无非就在点和线段上的3个点确定，两个端点和点到这条线段直线的垂线相交的点，当然，如果相交的点不在线段上，则最短距离就是两个点中的一个，否则就是点到这条直线的最短距离。

可以通过点积来判断点和线段的相对位置，并且利用叉积计算出点到直线的最短距离,比如上图2，ABxAC为一个平行四边形的面积，而这个面积又等于|AB|*h,h就是C点到AB所在直线的最短距离。代码如下：

double Dist2Seg(point c,segment AB)
{
    if(AB.pa.x==AB.pb.x && AB.pa.y==AB.pb.y)
        return dist(c,AB.pa);
 
    double d=abs(cross(AB.pa,AB.pb,c)/dist(AB.pa,AB.pb));
    if(dot(AB.pa,AB.pb,c)<0)
        return dist(AB.pa,c);
    if(dot(AB.pb,AB.pa,c)<0)
        return dist(AB.pb,c);
    return d;
 
}

未完待续。。。

注：图片和相关资料来自wikipedia和TC Algorithm Tutorial

1.Wikipedia关于点积和叉积。

2.TC Algorithm Tutorial 的计算几何部分。

计算几何初步 - March 19, 2011 -